Relationship of Plating Thickness to Current/Amperage

A. Hi Krishna. Sorry, the "Electrochemical Equivalents" chart in the Metal Finishing Guidebook is in English units, not metric. But it does at least give you the factor 1.095 grams per amp-hour for nickel (at 100% efficiency). I don't know of any availability of that chart in metric, but if your team generates it we'll be happy to post it :-)

Meanwhile, you can calculate it for nickel from Faraday's Law and the example on this thread. Luck & Regards,


Ted Mooney, P.E. RET
Striving to live Aloha
finishing.com - Pine Beach, New Jersey

A. Hello, Leah. "Faraday's Law of Electrolysis" explains it. It says that one Faraday of electricity (96,485 ampere-seconds) will electrodeposit one gram molecular weight on the cathode.

Usually available on eBay;

sometimes on
AbeBooks or Amazon

(affil links)
free pdf is currently available from academia.edu

A. Hello again Leah. I'm not sure whether I am misunderstanding you, or you are misunderstanding me, but there is little more to say about the relationship between the amount of electricity used and the quantity of the deposit after Faraday's Law has been introduced because it explains the simple science behind it: if you pump "x number" of electrons (measured in ampere-seconds) through the external wiring from the anode to the cathode, an equal number of positive charges must flow from the anode to the cathode to balance it. The general way that this occurs is the resulting metallic ions (which were stripped of some of their electrons) oxidize & dissolve into solution, and migrate across to the cathode, where they are reduced to metal again when they re-meet the electrons.

In actual practice, though, some portion of the excess electrons at the cathode can't wait for the metal ions from the anode to reach them and will instead pull an H+ ion out of the aqueous (H20) solution, leaving behind an OH- ion. For each two H+ ions pulled from solution, one molecule of H2 gas will evolve at the cathode. The percentage of the applied current which actually deposits metal is called the "efficiency". Chrome plating is notoriously inefficient, maybe 12-25%, but many plating baths are 90-99% efficient if operated at low current. Efficiency cannot be maintained at high currents because, if you try to plate too fast, metal ions will not be able to migrate across the solution and through the boundary layer quickly enough to keep up, and more H+ ions will have to be be pulled out of the solution.

There are stock formulas for how to "run the numbers" for Faraday's Law when dealing with an alloy like tin-lead, which consists of multiple metals with different molecular weights.

Also charts have been prepared that take the density, atomic weight, and valence of the specific metal into account, and apply all the necessary conversion factors, so you can simply read the thickness of deposit vs. amp-hours per square foot in a very straightforward format (these charts assume 100% efficiency). Such a chart is in the appendix of the Metal Finishing Guidebook.

More power ... but not so much that the efficiency drops :-)

A. Leah,

So, you are a cadet engineer striving to be a plating engineer. I bet this is one of your projects.
Regarding your inquiry, you must read a good book on plating. There is one in National Bookstore, or ask Engr. Raul Danganan, he is a good college professor here in Cebu.

Good luck on your search.

A. Leah.

I plate tin/lead and tin; as long as it is acid-based using the formula: 7.8 x thickness x 60 divided by current density gives you thickness. 7.8 are the amp hours to deposit .001 of material.

Let's use .0003 as the thickness you desire. 60 is a constant and means minutes; the answer is in minutes to deposit your thickness.

(e.g.,) 7.8 x .3 x 60 / 20 (asf) = 7 min works for me.

A. Thickness = [I,amps * t, sec * milli-equiv] / [96485 * Density * Area]

You can also use Fick's second law to compute for the correction factor which is dependent of the type of chemistry you are using. Fick's second law is discussed in Chemical Engineering Kinetics. Get the principle and apply it. You can also use the above equation to get the rate by assuming it's first order. You must also have a good knowledge of your line's efficiency to correlate your off-line evaluation with future on-line runs.

Sana makatulong.

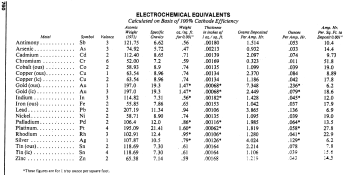
A. Hi Casey. We appended your query to similar ones, and the quick answer to your question is that the chart you are looking for is in the appendices of the Metal Finishing Guidebook, and is entitled "Electrochemical Equivalents".

Sorry, but in order to not violate copyright, the graphic has been deliberately reduced to illegibility here so you can see what document you are looking for while not being able to use this graphic as a substitute for it. But for now at least, you can dwnload the Metal Finishing Guidebook per the link posted earlier. Good luck.

Regards,

A. The calculations as described on the answers that Ted attached are correct, provided that the current efficiency is 100%. If the current efficiency is < 100% then you must divide the result by the % efficiency. Nickel, for example, plates at 95-97% efficiency. So, at 40 amps/square foot, it takes just under 3 minutes to plate a coating 0.001" thick (2.8 grams/square foot). For acid tin @ 100% efficiency, at 20 ASF it takes 23 minutes to plate 0.001". For 90/10 lead-tin @ 20 ASF, 21 minutes.

I have found it useful to plot the current density on the Y axis vs. grams deposited per unit area on a log-log graph. The result is a straight line with a slope of -45 degrees. With this graph, if you know the minutes to deposit 0.001" at one current density, you can read the minutes required at any current density.

A. All good advice - except that you will only calculate the average thickness. More will deposit on edges and less in recesses.
To accurately know the thickness at any point it is necessary to measure it. To repeatedly achieve the thickness you must keep the jigging, current density, etc., constant.
If it was simple to predict the thickness accurately, platers would not spend vast sums of money on kit like x-ray fluorescence spectrophotometers.

P.S. Lyle's graph will only be 45 degrees if you choose the right scale.

A. Hi Mouli. Please tell us what metal or exact alloy you are electrodepositing, and what units you are expressing current density and time in, and then we can show you the whole derivation. Your factor starts with the Faraday constant of 96485 from Faraday's Law, and then conversion factors involving valence, atomic weight, and density (and maybe 'efficiency') are combined produce the 0.22 figure.

Regards,

A. Welcome back Mouli. If you read the page about Faraday's Law, even if you don't fully understand it, you will realize why your estimate of
"Thickness of plating in microns = 0.22 * A/sq/dm * minutes of plating time"
can only apply to one particular metal or alloy and is not valid for any other metal. That's why we need to know what metal you have been using it for before we can explain its derivation with numbers.

But for zinc, for example, with its atomic weight of 65.38 and its valance is 2, a Faraday of electricity will deposit
65.38/2 = 32.69 grams of zinc
But 1 amp x 60 seconds is only 60/96485 Faradays, so it will deposit 60/96485 x 32.69 = .02033 grams of zinc
The density of zinc is about 7.14 grams/cu.cm, or 7140 grams/cu.dm, so 1 amp-min deposits about 0.2033/7140 = .00000285 cu.dm of zinc
So, if the area plated is a square decimeter, the thickness plated is .00000285 dm or .285 microns
So for zinc plating at 100% efficiency the formula would be:
"Thickness of plating in microns = 0.285 * A/sq/dm * minutes of plating time"

We might estimate the efficiency of alkaline zinc plating at 77%, and therefore multiply the 0.285 x .77 and arrive at
"Thickness of plating in microns = 0.22 * A/sq/dm * minutes of plating time" :-)
However, I'm sure you can see that "0.22 is the answer, what is the question?" isn't really valid :-)

Regards,

A. Hi, Sunil. If you read the earlier postings you'll see links to a chart in the Metal Finishing Guidebook for a quick answer, and to Faraday's Law for the full theory and understanding.

But as you know, 1 micron in 1 hour is ridiculously low and very wrong. My suspicion is that you are doing alkaline tin plating, and are not aware of the need to 'film the anodes'.

GS Branch AESF "Electroplating Course Manual"

Luck & Regards,

A. Hi. Please start by studying in detail the 2-page training manual I already posted regarding filming the anodes. What I posted is by far the most detailed coverage of the subject that I am aware of. It may be necessary to retain a consultant to offer hands-on training if no one there has stannate tin plating experience or this is not understandable.

Luck & Regards,