Surface Area Calculation for threaded rod

A. bob,

I have always used and have found the following formulation to be quite accurate.

take the bottom pitch diameter of the rod

use it in this equation

3.14 X diameter X length X 1.5

ray

A. Excluding electroless plating, the exact surface area is technically irrelevant because the peaks of the thread will plate several times more than the valleys will, even if you tweak the bath to be a very slow one.

A. It's quite easy; just use this (lateral area)=(b)L (Total area)=(b)L+b

A. I made a quick mathematical calculation and a simulation on CAD software and the results are quite close:

A=3.14*L*D*1.625 Where D is the pitch diameter and L the length of the portion threaded.

Which is not very far from the answer I saw before with the 1.5 factor.

If you are interested by the method used, search for Guldin's theorem.

A. Hi norazma. If you google for "surface area of a cylinder" you will find lots of easy to follow explanations and animations.

As you will hear in those animations: the ends of a cylinder are circles; the area of a circle is 3.14 x diameter²/ 4; there are two ends; so the total area of the two ends put together is 3.14 x diameter²/ 2. But when you are plating a long rod, the area of the ends compared to the rest of the rod might be insignificant, and might be ignored. In the formulas that you are quoting, they were ignored ... people are talking about the surface area of a cylinder, ignoring the ends: which is then 3.14 x diameter x length.

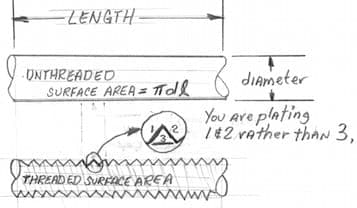
So, if the surface area of a non-threaded rod, ignoring the ends, is 3.14 x diameter x length, what would be the surface area of the same rod after it is threaded? Well, you would have to multiply by a factor that takes into account the fact that the rather triangular shape of the thread adds area that must be plated. If threads were the exact shape of an equilateral triangle, you would be plating two of the sides instead of the base, so that adjustment factor would be 2.

It would depend on the exact threading profile, but the readers have estimated that factor at 1.5 or 1.625. Not knowing better, I'd estimate it at 2. But James Watts' earlier comment is very appropriate because trying to determine the surface area of a threaded rod for electroplating purposes can quickly lead to the old bugaboo of precision without accuracy. If you are electroplating it, whether it's closer to 1.625 or closer to 2 is not going to be important for practical purposes :-)

Regards,

A. The calculation of surface areas of manufactured articles has been an enduring area of interest for me since I began my career in surface finishing in 1978. This interest evolved from my involvement in mechanical plating and mechanical galvanizing, an area in which I have a significant amount of experience and expertise. In these processes, the surface area of the articles to be plated must be known before the commencement of the process as the components are added in direct proportion to the surface area. Over-addition or under-addition may result in defective or deficient production.

"Surface Area Formulas and Tables"
by Tom Rochester

Over the past 35+ years I have calculated the surface areas of thousands of parts as a service to our customers, and I know that many companies have used my calculations for other surface finishing process for almost as long.

I have now written, and my company, Plating Systems and Technologies, has published this month (June 2016), a new book entitled Surface Area Formulas and Tables. This book includes over 50 formulas and calculated surface areas for thousands of parts that are often plated, as well as rules of thumb for estimating surface areas. It also includes technical/economic models for a number of surface finishing processes as well as other related information. Ted Mooney, the esteemed proprietor of this website, has had the opportunity to view a prepublication copy. It also includes a variety of applications for surface area information.

With regards to Bob Holderman's inquiry posted earlier in this thread, in order to calculate the surface area of a threaded article within a few percent, it is mandatory that the article be able to be physically measured and examined. The reason for this is that the range from the lowest acceptable dimensional limits for major and minor diameter (as well as, of course, the pitch diameter) and the highest acceptable limits can yield a surface area that can vary by over 5%. (For some articles manufactured to specification, the variation can be over 20%.) A quick look at the UN thread profiles would be instructive. The best single source for dimensions of thread forms and threaded fasteners is Machinery's Handbook [on Amazon affil links]; excellent information is also available from organizations such as the ASTM, DIN, IFI and a number of others.

To return to the original question about the surface area of threaded rods - The area of a cylinder is easily calculated using easily available mensuration formulas (available online or from readily available handbooks). As a rule of thumb, the area of a rod or wire form in square feet per hundred pounds can be estimated as 10 divided by the diameter in inches. (This ignores the area at the end of the rod or wire.) Thread forms will have 75% more area (more or less); it depends on the exact dimensions of the thread form (for example, fine threads have less surface area than coarse (UNC and variants).