Sound technical content, curated with aloha by
Ted Mooney, P.E. RET
Pine Beach, NJ
The authoritative public forum
for Metal Finishing since 1989
-----
Crowsfoot with torque wrench. What's the math?
I am confused about where you grip the wrench being inconsequential. I had my torque wrench at an Air Force PMEL lab to check its accuracy. With my hand in the recommended location, it was shockingly accurate. When I moved my hand the calibrator's reading changed. I was really surprised this happened as I assumed where you held the wrench didn't really matter, the force of the spring had to be overcome and intuitively it seemed if I held the wrench in a different spot, it would just change the amount of force I needed to make the wrench break. But the calibrator showed me it did matter, and we're not talking single trials, this was 10 trials each. Can you explain what is happening with this? Is it the calibrator/wrench interaction, or is hand position important as it would seem from what I saw?
Also - I got rid of my cam and spring units and replaced them all with strain gauge units that don't break at all, but I am still very careful to apply force as Snap-On has marked on the grips.
- Duluth [Texas]
February 28, 2022
A. From what I've been taught in my Duke Energy course, many torque wrenches do not have the click mechanism aligned with the center of bolt rotation. This, much like using an extension device (crows foot) can change the actual torque on the bolt.
The equation T=(DS(A+B))/A is used to calculate the change in torque using an extension device with T being torque, DS being dial setting, A being distance from the center of where you hold the handle to the center of the socket adapter, and B being the distance from the socket adapter to the center of bolt rotation.
If B is 0 then A cancels out leaving T=DS. This doesn't seem to be the case with the wrench you used which would lead me to believe that the wrench has its click mechanism unaligned with the center of bolt rotation which, depending where you hold it, can change the value of A.
- Charlotte North Carolina
September 15, 2022
Ed. note: Since 1989 this forum has enjoyed the camaraderie & warm aloha which real names & locations afford. If you're not into that spirit, those who do post with their real name may be less likely to engage with you.
⇩ Related postings, oldest first ⇩
Q. I work in a small engine shop and I need some help. Does anyone know the math when it comes to using a crow foot on torque wrench? I have spent who knows how many hours on line looking and it seems that no one knows. Please help.
DAVID H [last name deleted for privacy by Editor]- Tryon, North Carolina
2001
A. Torque is actually a pretty simple concept. It's the force times the perpendicular distance from the point of application of the force to the axis around which you are applying the force. A 3-ounce force applied at a length of 6 inches from the axis generates 18 inch-ounces of torque; a 200 pound force exerted at a distance of 3 feet generates 600 pound-feet of torque. A 50 pound child sitting on a see-saw 3 foot from the bar will balance a 75 pound child sitting 2 foot from the bar.
The complication with a crowsfoot on a torque wrench is that the scale is calibrated to its center of rotation (where you would normally put a socket), but the lever arm (the perpendicular distance from the center of the bolt to the hand grip on the wrench) will be longer or shorter than that depending on how you apply the crowsfoot. To make it just a bit more complicated, the more force you put on a torque wrench, the more it twists--this doesn't effect the length of the lever arm in normal application where a socket is centered on the rotation point, but when using a crowsfoot, the length of the lever arm could actually increase or decrease as the wrench starts twisting.
In the example shown below, if the wrench reads 100 foot-pounds torque, the actual torque with the crowsfoot is 100 x 20/18 = 111 foot-pounds.
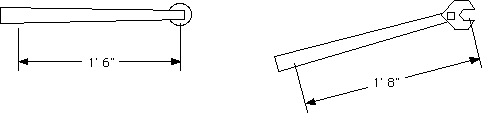
Because of this complication, some auto manufacturers warn you to use their specialized torque tools rather than using a crow foot on a torque wrench.
Ted Mooney, P.E.
Striving to live Aloha
finishing.com - Pine Beach, New Jersey
A. The torque wrench measures the torque or twist applied at the pivot point or where you would normally put on a socket which is centered on the pivot point. The crowsfoot .
is about a 2 inch extension on the other side of the pivot point, so it torque reading on the wrench is not the same as applied to the nut or bolt.
A firm that does torque wrench calibration could give you a cheat sheet or reference sheet of corrections for the one crowsfoot supplied at that calibration. The 5/16" is not going to be exactly the same fudge factor as a 9/16". Probably close enough for most work.
The cheap way to do it yourself, is to use a second torque wrench and run the crowsfoot against the normal one with a bolt and double nut part to join them up. I have never seen two torque wrenches exactly the same, so which one is right if you really care?
James Watts- Navarre, Florida
A. I ran across your question when searching for an inch lb torque wrench. I purchased a Husky brand from Home Depot. The instruction sheet has the formula for calculating the torque with a crowsfoot. E- Effective length of extension - measured along the centerline of the torque wrench. L Lever length of the wrench - center of grip to center of drive. T(W) - Torque set on the wrench. T(E)- Torque applied by the extension to the fastener.
T(W) = T(E)* L/L+E
T(E) = T(W)* (L+E)/L
I'm not endorsing Husky or Home Depot - I just provided those for fyi.
Todd E [last name deleted for privacy by Editor]- Glendora, California
A. If the crowsfoot is put on at a 90° angle and not at the end increasing the length, it will not effectively change the torque value. The overall length of the lever will be the same for the applied force.
Clayton R [last name deleted for privacy by Editor]- Amarillo, Texas
2002
That's an excellent point, Clayton. The length of the lever arm is not exactly the same in that case but it's very very close.
Ted Mooney, P.E.
Striving to live Aloha
finishing.com - Pine Beach, New Jersey
|
SOCKET EXTENSIONS Q. Hi, This is concerning an extension added to the socket. The extension is 2". Will it apply the torque set at the handle? This is a standard socket set extension;tubular. I read in a related post that horizontal extension will change the torque so this one is about a vertical extension.
Thanks for the help. Henry G [last name deleted for privacy by Editor]- Houston, Texas 2004 A. Those extensions have no effect on the torque reading and require no adjustment. Ted Mooney, P.E. Striving to live Aloha finishing.com - Pine Beach, New Jersey
- Houston, Texas |
Thanks Ted, guess I just missed the
"click" on the one broke screw.... :)|
|
LOCTITE Q. Does anyone know what is the effect of the application of threadlocker ⇦this on eBay or Amazon [affil links] on the torque value? Under normal circumstances, I apply a 100 ft-lb torque on a 1/2" diameter bolt. If I apply Loctite 243 , how much torque reduction would I need? Ceejay [last name deleted for privacy by Editor]- Singapore 2005 A. As a shipyard and home project worker I've used Blue threadlocker
⇦this on
eBay
or
Amazon [affil links]
on 1/2" fasteners, it is anaerobic (sets up in absence of oxygen). When set to required torque (35 Ft/Lbs, left for 15 minutes, checked for break to 8 ft/lbs and never found a break). For I 1/4"stud setting to standout and break check of 200 ft/lbs was always sat after 1 hour set time. - Norfolk, Virginia February 26, 2006 |
Q. I have a question about calculating torque? I have heard a lot about horizontal systems but what about vertical ones. I have to calculate the torque required on a telescoping wrench that is attached to a motor. Torque would be applied vertically as opposed to horizontally. I'm pretty sure that torque is a directional quantity. I am however stuck on this. I used the standard equation that you would use for a crowsfoot but I think that is incorrect.
Thanks,
- Brampton, Ontario, Canada
2007
by Roger Welsch
on AbeBooks
or Amazon
(affil links)
Q. This topic has me wondering about something very similar to this. I my 2006 Harley service manual they mention using a Torque Adapter for tightening the rear axle nut. I'm sure this adapter was developed to keep from having to remove the right side muffler during belt tensioning. In the photo this adapter appears to be about 6" long, and they stress the point of it needing to be 90 deg. to the torque wrench centerline. The puzzling part is that they also specify the exact same torque reading as my 2003 service manual that does NOT have the torque wrench adapter. Does having the adapter at 90 deg keep the readings the same? Or is there some sort of calculation that should be done to provide the correct torque?
Ron R [last name deleted for privacy by Editor]- Janesville, Wisconsin
A. "Give me a lever long enough and a fulcrum on which to place it, and I shall move the world." -- Archimedes.
Torque is the product of force and the length of the lever arm, so it is essential that the length of the lever arm be right. The length of the lever arm is the perpendicular distance from the applied force to the center of rotation, and that will remain the same if the attachments are kept at 90 degrees.
Ted Mooney, P.E.
Striving to live Aloha
finishing.com - Pine Beach, New Jersey
|
|
DOES TWISTING IN LONG EXTENSIONS AFFECT TORQUE Q. I know in theory, that a socket extension should not affect the torque transmitted to the driven equipment (bolt, etc). However, on large bolts and nuts that we torque at our power plant, we have to add long socket extensions (~ 1.5 to 2 feet) to reach the bolt or nut. I am thinking that an extension this long will twist some, and that will reduce the amount of torque delivered to the load. Are there any tables or charts or even rules of thumb to account for this? RANDY DEHARTPower Plant - Paducah, Kentucky 2007 A. Having a long extension will not affect the torque reading if the extension has twisted as much as it wants to twist for a particular applied torque. - Merrillville, Indiana |
Q. I'm not sure if you ever got your question answered or not. Seemed that not everyone know what a "crows foot" wrench is. Go to
www.norbar.com/torquewrenchextensioncalculator.php
^new address:
www.norbar.com/Calculators/tabid/57/Default.aspx^ new NEW address: see entry of Feb. 9, 2009 then enter the measurements that you are working with and it will make the calculations for you. The "crows foot" is simply an extension of the torque wrench. Try it out, it's pretty cool!
- Ozark, Missouri
2007
A. Here is the formula: M1 = M2 x L1 / L2
Where:
M1 is the torque setting of the wrench.
M2 is the actual torque applied to the nut
L1 is the normal length of the wrench
L2 is the extended length of the wrench (Length of wrench + length of adapter)
Example:
M1=torque wrench setting ?
M2=80 FT-LBS (Desired torque)
L1=18" (Length of torque wrench)
L2=22" (Total length of wrench with 4 inch extension added to wrench)
80x18/22=65.45 M1 therefore = 65.45; In other words if you want to torque a fastener to 80 FT-LBS using an 18 inch torque wrench with a
4 inch torque extender you will set the wrench to 65.45 FT-LBS
airframe and powerplant mechanic - Kalispell, Montana
Q. I am attaching a housing using 10 capscrews. The required torque is 70 - 75 ft lbs. Two of the 10 bolts are hard to get to and require a swivel socket with a 4" extension. Do I need to increase or decrease the torque on the wrench to account for this difference in order to attain the final torque of 70 -75 ft lbs?
Thanks
Bob
shop - Climax, Michigan
2007
A. Ron R,
Using a torque wrench adapter that is offset from the square drive at 90 degrees is not exactly a one-to-one reading with the torque wrench setting but is close enough that the difference is usually discounted. The longer the adapter the more the difference though! I believe the torque wrench offset adapter calculator at cncexpo.com/TorqueAdapter.aspx calculates the 90 degree angle correctly if you're interested.
- Seattle, Washington
On-Line Torque Wrench Crowfoot Extension Calculator:
www.belknaptools.com/extcalc.asp
- Wixom, Michigan
July 30, 2008
(you are on the 1st page of the thread) Next page >
Q, A, or Comment on THIS thread -or- Start a NEW Thread